結晶 3斜晶系(h k l)面の面間隔導出とキッテルの感想
久しぶりのエントリーです
しばらくバタバタしていてラズパイ関連あまり進められてません。残念。
とりあえずエセでもプログラムできますと言うために現在Pythonの本1冊勉強中です
さて、今回の内容はドタバタの原因の1つでもある固体物性論のレポートについて
「3斜晶系の(h k l)面の面間隔dを基本並進ベクトルa,b,cの大きさa,b,c、ベクトルa,bのなす角をγ、b,cのなす角をα、c,aのなす角をβを用いて表しなさい。」
という内容
言い換えてしまえば、
7つの結晶系の面間隔の一般式を導出してね
ということです
導出の流れと参考にしたもの等々メモしておきます
固体物性論の参考書について
とにかく復習だ、とノートをペラペラ見ますが分かるようでスッキリしない
そこで参考書を買おうと固体物理参考書界で知らない人はいないこの本を購入しました

- 作者: チャールズキッテル,Charles Kittel,宇野良清,新関駒二郎,山下次郎,津屋昇,森田章
- 出版社/メーカー: 丸善
- 発売日: 2005/12/01
- メディア: 単行本
- 購入: 1人 クリック: 5回
- この商品を含むブログ (10件) を見る
本という存在の全てが好きなので名著といわれるものはいわば大好物です
早速読んでみますが...日本語が回りくどい
図がたくさんあって理解の助けになるのかと思いきや、図の説明文がわかりにくい
わかりました、これは名著ではありますが初学者向けとは言い難そうです
固体物性の何たるかがわかっていないのに手を出した僕が悪かった
ということで今回はノートをさらっと見返す復習にとどめ、初学者向けの参考書はまた探しましょう
とにかく目先のレポート内容に入っていきます
(h k l)面の面間隔を求める
結晶とは?
結晶は原子や分子が空間的に周期性を持って規則正しく配列したものです
その周期性の1単位となりうるものを結晶構造と言って良いでしょう
結晶構造は
- 空間格子と単位構造の組み合わせ
- 単位格子の積み重ね
という2通りの考え方で説明できますが、一般的に2の単位格子をよく使います
単位格子を表現する
単位格子は3つの線型独立なベクトルで表すことができます
この3つのベクトルを基本並進ベクトルと呼びます
a,b,cで表すことにしましょう
逆格子空間を導入する
フーリエ変換は時間tの空間と周波数ωの空間を繋ぎます
似たような関係として、実格子空間(実際に格子が存在している空間)と双対関係をなす逆格子空間というものを考えるようにします
逆格子空間を考えるメリットは
結晶構造と波動の相互関係が取り扱いやすくなること
です
現代の半導体技術を支える様々な材料の解析に役立つんだと考えておきましょう
この逆格子空間でa,b,cに対応するベクトルをa*,b*,c*と表して、逆格子ベクトルと呼びます
数式をブログ中でうまく書く術は今はまだ勉強する暇がないので見にくいですが、
(LaTeX習得のためブログ中に数式を入れられるようになりましたが現在全て直す時間がないので少しずつ直してます 2018/07/23)
逆格子ベクトルは以下のように表されます
スカラ3重積が分母に来て、分子には2πと外積が乗ってます
この辺りは調べると詳しい解説あると思います
格子面の表現
格子面は格子点を無限個含む平面と表現できます
また、格子面自体無限個あるのでうまく区別して表現しましょう
基本並進ベクトルa,b,cをそれぞれ整数h,k,lで割った3つのベクトルの終点を含む面を(h k l)面といいます
これで結晶構造中の固有の面を表現できます
ここで次のベクトルを定義しておきます
このベクトルは(h k l)面に垂直であるという重要な性質を持っています
面間隔の表現
(h k l)面は結晶中の固有の面の表現ですが、面を表現しているに過ぎません
結晶中にはある1つの(h k l)面に平行な面が無限個あると言えます
そこで最近接面間の距離はどの2面を考えても同じであるのでこれを面間隔とします
先ほどの に関する性質から
は例えば次のように表せます
これを計算することで結局dhklは次のように表現できます
これを用いて計算を進めていきましょう
具体的な計算
先ほどの式はの計算が非常に面倒です
しかし、これまで定義してきた値を用いて計算は可能です
非常に綺麗にまとまったページがあったので具体的な計算は以下のリンクを参考にしましょう
3斜晶系の体積
これも少しややこしいです
3つのベクトルが張る平行6面体の体積がすなわちスカラ3重積ですが、今回の場合はと
のなす角が簡単にはわからないため工夫が必要になります
反変ベクトルと共変ベクトルの関係を用いると比較的簡単に求めることができるそうですが、僕はこのあたりの勉強がまだなので分かる人は以下のリンクを参考にしましょう
誰でもわかる求め方を以下に示します
まずこんな感じに直交座標系と基本並進ベクトルをイメージしましょう

先に大枠の考え方を示します
のz成分(以下でfと定義する)を求める
と
がつくる平行四辺形の面積を求める
- 1と2で高さと底面積を求めたことになるのでそれらの積が体積となる
以上です。考え方は中学生でもわかりますね
では、記事の初めの設定をもう一度思い出しましょう
「基本並進ベクトルa,b,cの大きさa,b,c、ベクトルa,bのなす角をγ、b,cのなす角をα、c,aのなす角をβ」
です
これらと図から各ベクトルを成分表示します
a = (a,0,0)
b = (bcosγ,bsinγ,0)
c = (d,e,f) (d>0 , e>0, f>0)
次に、cの大きさ、a,cの内積、b,cの内積を考えることで以下の式が成り立ちます
d2 + e2 + f2 = c2
accosβ = ad
bccosα = dbcosγ + ebsinγ
この3式の第2式、第3式よりd,eがそれぞれ求められるので、これらを第1式に代入することでfの値が得られます
以上で「高さ」は求められました
次に「底面積」ですが、これは簡単でaとbの外積の大きさがそのまま底面積の値になります
底面積Sとすれば
S = absinγ
です
あとはfとSの積を計算すれば体積Vが求められたことになりますね
このVを先述の面間隔のリンク先の結果式中のVに代入すれば面間隔の一般式を完全に得たことになります
非常に複雑な式ですが以下に示しておきます
画像でしか貼れないのはすみません...いつか勉強します
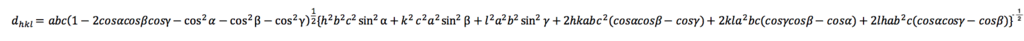
まとめ
今回は結晶の面間隔の導出をまとめました
面間隔の表現のために逆格子空間の概念を導入してあとはゴリゴリ計算!
という感じです
最終の式は煩雑ですが7つの結晶系全てに通用する一般式になっているので単純立方等の面間隔が容易にわかる結晶でパラメータを入れて計算してみるといいと思います
さて、ラズパイ工作の方はPythonの勉強が終わってから徐々に再開していきます
テキストはこれにしました
またこれの感想もあったらあげたいな
早くiPhoneでエアコンつけてから帰宅する夢叶えたい
